Golfing ARC-AGI with a Evolutionary Agentic Loop

Introduction

I went into the NeurIPS 2025 Google Code Golf Championship with zero prior code-golf experience—armed only with curiosity and a stubborn belief that a well-crafted agentic LLM loop could do the code golf for me. Instead of memorizing every byte-saving hack by hand, I built a lean, evolutionary agent and set it loose on the notorious ARC-AGI puzzle benchmark.

From the start, I was up against seasoned code-golf hobbyists and a leaderboard full of code golf veterans. For three months, my team and I tried everything: evolutionary solution databases, handcrafted code-golf templates, careful context engineering, and the occasional desperate manula crafted regex solution.

In the end, we finished 19th - but more importantly, we discovered what actually works (and what breaks) when you unleash an LLM-driven agent on competitive code golf.

This post is a practical field guide to that journey: how we built our agent, what finally moved the needle, where context rot kills you, and which human-injected templates turned into repeatable byte-savers. Whether you’re into LLMs, agents, or just love clever code, there’s something here for you—and maybe a template you’ll want to steal for your own golf game.

The Task!

At its core, this competition combines two objectives:

1. Solve each ARC-AGI puzzle correctly; and
2. Code-golf the working solution to the fewest bytes.

Understanding and solving an ARC-AGI task

ARC-AGI is a benchmark of grid-based abstraction-and-reasoning puzzles. Each task provides a handful of input→output examples on small colored grids. The goal is to infer a rule that generalizes to unseen inputs and to implement that rule in Python.

Here are some examples of the ARC-AGI tasks:

ARC-AGI Example 1

This is the Puzzle 1 of Arc AGI. Build a 9×9 grid arranged as a 3×3 grid of 3×3 blocks; For each 3×3 block at $(3*i,3*j)$ of the output, if the input cell $g_{i,j}\neq 0$, copy the entire 3×3 input into that block; otherwise fill that block with black.

ARC-AGI Example 2

This is the Puzzle 2 of Arc AGI. The patten of this specific task is to fill in every enclosed area of green point with yellow colour.

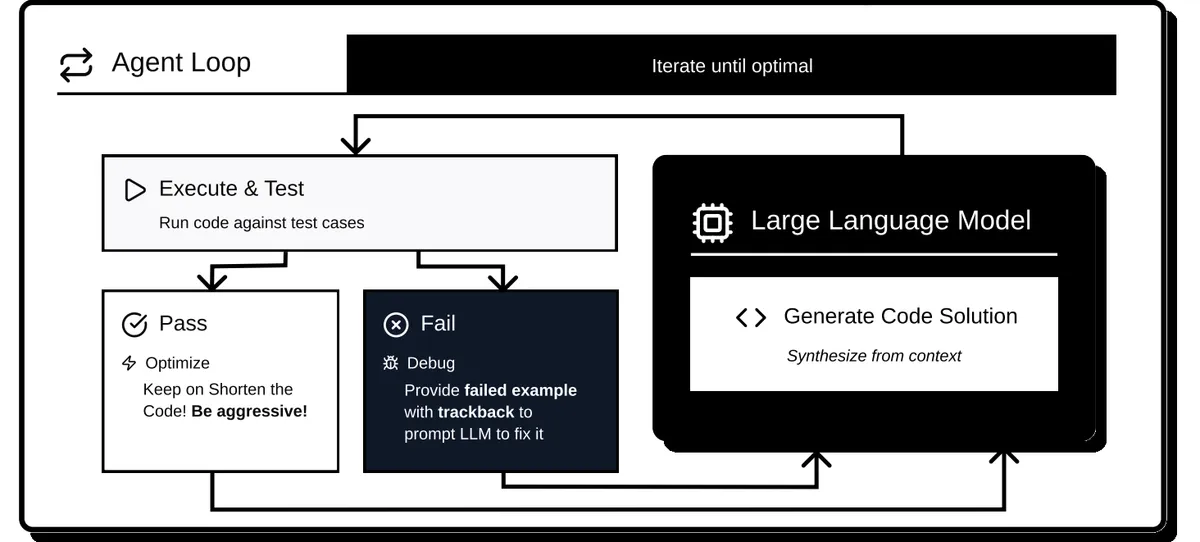
ARC-AGI Example 379

This is the Puzzle 379 of Arc AGI, The patten of this specific task is that we first need to extend each red dot toward the blue lines and then at which it intersect, we draw a blue square around the intersection.

Each puzzle is visualised as a coloured grid for readability; the underlying data are integer matrices with a fixed colour↔index palette (see mapping). This matrix form is what the Python code operates on.

For reference, the first input–output pair of Example 2 is:

At a glance, even humans need a moment to spot the rule in these examples. For LLMs, there are a few more factors that makes this even harder:

• Abstract, multi-step rules. Even humans pause to understand the pattern; ARC-AGI patterns are often abstract and compositional, causing LLMs to hallucinate heavily.
• Numeric form, spatial semantics. The inputs are matrices, but the underlying logic is more about spatial layout than arithmetic. LLMs, trained and heavily RL on mathematical problems, often misalign with or get confused by these topological tasks.
• High task diversity. With hundreds of distinct patterns, manual labeling or human-in-the-loop hints isn’t truely feasible. The LLM has to work it out alone.

To address these challenges, we experimented extensively with context engineering, crafting the right prompt context, balancing informativeness with brevity to avoid context rot. More details are in the context engineering section.

Code Golfing of working solution

Once correctness was locked in, the goal was to minimize byte length. Many standard code golf tricks help with this—like removing spaces, or using patterns such as:

1
for i in (1,2,3):
2
# instead of
3
for i in range(3):
4
# to save 1 byte

or

1
x>0<y
2
# instead of
3
x>0 and y>0

There are dozens of such tricks, but the real art of code golfing is escaping local minima. Beyond a point, saving a single character often requires a complete logic rewrite. In the final stages of the competition, trimming 1–2 bytes usually demanded a new approach.

For example, here’s our best solution for task 1:

1
p=lambda g:[[A&C for A in A for C in B]for A in g for B in g]

While the public best solution (3 bytes shorter) is:

1
p=lambda*g:[[*g,min,p][2](r,s)for r in g[0]for s in g[-1]]

Absolutely mind-blowing 🤯 (at least for me).

This gap led us to adopt two key tactics: (i) a living code golf idiom cookbook to teach byte-saving patterns, and (ii) a lightweight evolutionary database to seed the agent with diverse prior solutions, helping it escape local minima while preserving correctness.

My Agent

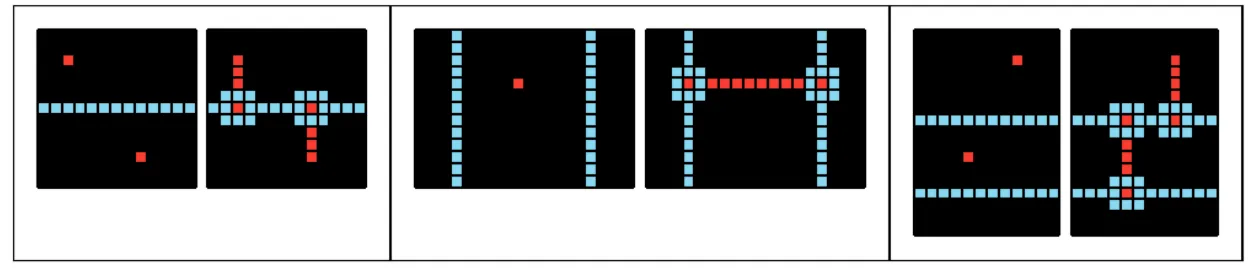
Given these challenges, the architecture below delivered reliable working solutions in the early stages, and consistent byte minimization in the later phases of the competition. At a high level, the system comprises three cooperating components (Fig. 1): an Evolutionary DB for retrieval and diversification; a Context Engineering stage that assembles the system prompt (role, task specification, ARC-GEN snippets, cross-task exemplars, golf idioms); and an Agent Loop that proposes code, runs tests, ingests failures, and retains the shortest correct program.

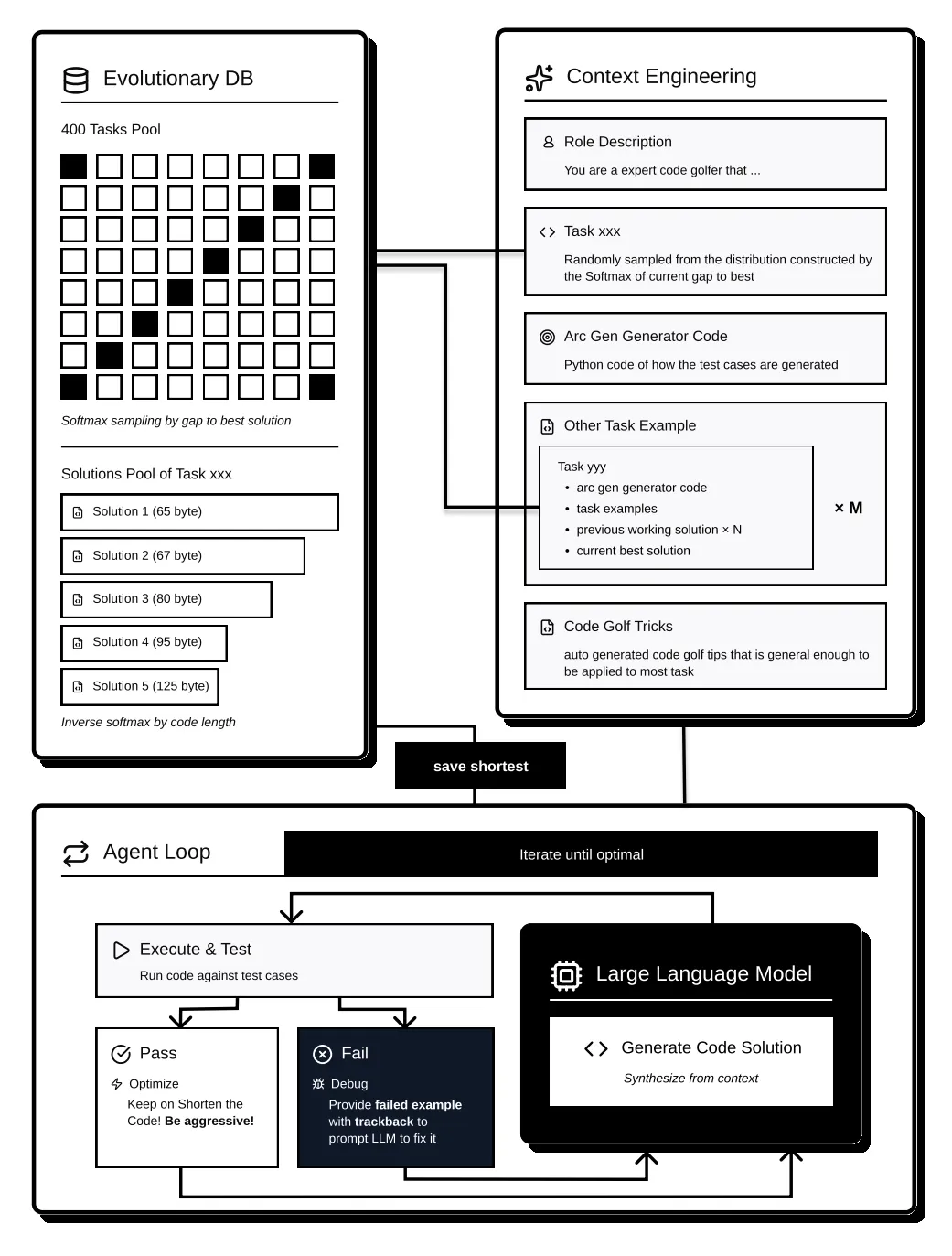Figure 1: Architecture overview. The Evolutionary DB supplies tasks and prior solutions; Context Engineering assembles the prompt (role, task spec, ARC-GEN snippets, exemplars, golf idioms); the Agent Loop executes proposals, feeds back failures, and saves the shortest correct program.

Components at a Glance

• Evolutionary DB.
  A pool of 400 tasks, each with its current best (lowest-byte) solution, plus a per-task set of correctness-verified prior LLM solutions that are longer than the best. These longer solutions are used for diversification and crossover.

• Context Engineering.
  More a stage than a standalone component, this phase assembles the system prompt by experimenting with different sources of information to help the LLM better understand the task. The final prompt includes concise role instructions (as an expert code-golfer), the current task specification and ARC-GEN generator, a small selection of other tasks (with examples and best or near-best solutions) to induce transferable knowledge, and a golf idiom cookbook (safe, broadly applicable byte-saving patterns).

• Agent Loop (LLM + tools).
  The LLM proposes code; a toolchain executes it against generator-defined tests, measures byte length, and returns tracebacks and failing I/O pairs on error. Passing proposals are compared to the best solution; the shortest correct solution is persisted and pushed back to the DB.

Agent Loop

This was the straightforward part: the system is essentially a program-synthesis loop tailored for ARC-AGI code golf. We designed this agentic loop to be as lean as possible, offloading most of the heavy lifting to Context Engineering and the Evolutionary DB. This was largely out of necessity, as we relied primarily on Gemini’s generous free tier (with occasional experiments on OpenRouter to test alternative models within a tight budget). To keep costs and latency down, we avoided heavy add-ons (like long-horizon planning, persistent memory, or code search) that would increase the number of LLM calls. The simple loop above gave us fast iteration, predictable costs, and let the LLM do the real work.

To build this lean agentic loop, we equipped it with a few essential tools:

• Extract code from LLM outputs (strip reasoning, capture the final Python block or code delimited by markers).
• Validate the snippet: ensure it defines a single entry point (p(g) or p = lambda g: ...), uses only the Python standard library, and parses without syntax errors.
• Run and score against task examples. On failure, return a concise traceback and the failing I/O pairs.
• Minify/normalize with python-minifier for easy byte wins (whitespace, imports, constant folding, safe name shortening), then measure the final byte count.

Thus the entire agent loop can thus be described as:

1. Prompt the LLM with the system + user context to propose code.
2. Extract → validate → minify. If invalid, feed back a short reason (syntax/import/entry-point).
3. Execute tests.
   • If pass: compare byte length to the incumbent; if shorter, persist as new best. Then asking it to continue shorten it.
   • If fail: return the traceback + failing I/O pairs as the next user message.
4. Iterate until the iteration budget is exhausted or no improvement for (K) rounds.

Here are some Validator guardrails that we checked when the LLM produced an answer:

• Enforce def p(g): ... or p = lambda g: ... only; no top-level I/O.
• Ban imports except safe stdlib used implicitly by the runner; no network/FS.
• Cap runtime per test; kill on timeouts; treat exceptions as failures.
• Normalise newlines and encoding before measuring len(code.encode()).

Evolutionary DB

The Evolutionary DB is a lightweight index over tasks and solution variants, supporting both crossover and diversification. It stores per-task metadata and a history of correctness-verified working solution of each task (including longer variants), which seed structurally diverse rewrites.

Data model (per task):

• best_bytes (our best), public_best_bytes (if known), solved flag
• solutions: correctness-verified programs
• last_updated, optional pattern_signature for similarity search

Sampling for a new iteration:

1. Pick a focus task. This is the task the agent will attempt to solve or further shorten. Prefer tasks with room for improvement or those not yet solved. Sampling uses a softmax over the margin:

   $$\begin{align} m(t) &= \begin{cases} \text{public\_best\_bytes}(t)-\text{best\_bytes}(t), & \text{if solved}\\[2pt] M, & \text{if unsolved (large constant)} \end{cases}\\ p(t) &\propto \exp\!\big(\beta\,\mathrm{norm}(m(t))\big), \end{align}$$

   where $\beta$ controls exploitation vs. exploration.

2. Retrieve in-task priors. From the focus task’s archive, sample $N$ prior solutions with an inverse-length bias to favor concise patterns but maintain diversity:

   $$p(s\mid t) \propto \exp!\big(-\gamma\cdot \text{bytes}(s)\big).$$

3. Add cross-task exemplars. Select $K$ additional tasks to import transferable knowledge and help escape local minima. Early on, these were chosen at random; later, we switched to pattern-similarity retrieval via extracted pattern tags.

4. Crossover from priors. Include the best solution and a small set of diverse, correctness-verified working solutions from the selected exemplar tasks. These offer a record of how other tasks were golfed, allowing the model to transfer byte-saving motifs or refactor logic to the current task and synthesize a shorter, behavior-equivalent program.

5. Mutate. The LLM proposes a candidate; we run deterministic tests, capture failing I/O and tracebacks, and measure byte length post-normalization.

6. Update the DB. Any correct candidate is added to the archive; if it beats best_bytes, it becomes the new incumbent.

This loop is easier to grasp with an example. Here’s how a sample prompt is constructed from the Evolutionary DB:

In this case, the DB selects Task 1 as the focus task, and retrieves several additional tasks (Tasks 239, 261, 397) as cross-task exemplars. The prompt begins by defining the role (“expert Python code-golfer”), then lists working solutions for each exemplar, and finally presents the focus task with a few of its prior working solutions. The prompt ends with a direct instruction to the LLM: synthesize a shorter program that still passes all tests—without copying existing code.

1
## Role
2
You are an expert Python code golfer.
14 collapsed lines
3
Your goal is to iteratively shorten working solutions while preserving their exact functionality.
4
Focus only on minimizing **code size in bytes**, not efficiency or readability.
5

6
## Learning From Past Tasks
7
You will be shown several solved tasks.
8
Each includes:
9
- One or more working solutions (sometimes with an improved, shorter version)
10

11
Study how the improved versions reduced code size.
12
Use these patterns to guide your approach for the current task.
13

14
## Example Tasks
15

16
===
17
Task 239:
18

19
You are tasked with producing the **shortest possible Python solution (in bytes)** that passes all the given test cases.
20

21
The current global best solution size is 99 bytes.
43 collapsed lines
22

23
## Generator Function
24

25
This is the generator function used to create the puzzles that our solution function `p` is trying to solve for this specific task:
26

27
def generate(width=None, height=None, colors=None):
28
  """Returns input and output grids according to the given parameters.
29

30
  Args:
31
    width: the width of the grid
32
    height: the height of the grid
33
    colors: a list of digits representing the colors to be used
34
  """
35
  if width is None:
36
    width, height = common.randint(3, 4), common.randint(3, 4)
37
    colors, color_list = [0] * (width * height), common.random_colors(9)
38
    while True:
39
      left, right, top, bottom, idx = 0, width, 0, height, 0
40
      while left < right and top < bottom:
41
        for r in range(top, bottom):
42
          for c in range(left, right):
43
            colors[r * width + c] = color_list[idx]
44
        didx = 0
45
        if common.randint(0, 1): left, didx = left + 1, 1
46
        if common.randint(0, 1): right, didx = right - 1, 1
47
        if common.randint(0, 1): top, didx = top + 1, 1
48
        if common.randint(0, 1): bottom, didx = bottom - 1, 1
49
        idx += didx
50
      counts_to_colors = {colors.count(x): x for x in colors}
51
      if len(counts_to_colors) == idx: break
52

53
  counts_to_colors = {colors.count(x): x for x in colors}
54
  counts = sorted(counts_to_colors.keys(), reverse=True)
55
  grid, output = common.grid(width, height), common.grid(len(counts), counts[0])
56
  for r in range(height):
57
    for c in range(width):
58
      grid[r][c] = colors[r * width + c]
59
  for idx, count in enumerate(counts):
60
    for r in range(count):
61
      output[r][idx] = counts_to_colors[count]
62
  return {"input": grid, "output": output}
63

64
This generator creates the input/output pairs that define the puzzle pattern.
65

66
Here is version 1 (168 bytes):
67
from collections import Counter
68
def p(j, R=range):
69
 c = Counter(sum(j, [])).most_common(9)
70
 return [[c[w][0] * (r < c[w][1]) for w in R(len(c))] for r in R(c[0][1])]
71

72
Here is version 2 (134 bytes):
73
p=lambda g:[[v*(r<n)for n,v in C]for l in[sum(g,[])]for C in[sorted({(l.count(i),i)for i in{*l}})[::-1]]for r in range(C and C[0][0])]
74

75
Here is version 3 (111 bytes):
76
def p(g):s=sum(g,[]);m=s.count;c=sorted({*s},key=m)[::-1];return[[i*(j<m(i))for i in c]for j in range(m(c[0]))]
77

78

79
The solutions show progressive improvement: from 168 bytes (version 1) to 111 bytes (version 3), saving 57 bytes total.
80
You should learn from this progressive improvement to further shorten the code that I care about in the current task.There is still room for improvement compared to the global best solution: 12 bytes can potentially be saved (from 111 to 99 bytes).
81

82
===
83
Task 397:
84

85
You are tasked with producing the **shortest possible Python solution (in bytes)** that passes all the given test cases.
86

87
The current global best solution size is 121 bytes.
88

45 collapsed lines
89
## Generator Function
90

91
This is the generator function used to create the puzzles that our solution function `p` is trying to solve for this specific task:
92

93
def generate(colors=None, brows=None, bcols=None, size=10):
94
  """Returns input and output grids according to the given parameters.
95

96
  Args:
97
    colors: a list of digits representing the colors to be used
98
    brows: a list of vertical coordinates where the boxes should be placed
99
    bcols: a list of horizontal coordinates where the boxes should be placed
100
    size: the width and height of the (square) grid
101
  """
102
  if colors is None:
103
    num_boxes = common.randint(2, 3)
104
    while True:
105
      bcols = sorted([common.randint(0, size - 2) for _ in range(num_boxes)])
106
      wides = [2] * num_boxes
107
      if not common.overlaps_1d(bcols, wides): break
108
    while True:
109
      colors, brows = [], []
110
      for _ in range(num_boxes):
111
        num_colors = common.randint(2, 4)
112
        color_list = common.random_colors(num_colors, exclude=[common.green()])
113
        brows.append(common.randint(0, size - 2 - num_colors))
114
        colors.extend([common.choice(color_list) for _ in range(4)])
115
      touching = False
116
      for i in range(num_boxes - 1):
117
        if abs(brows[i] - brows[i + 1]) < 2: touching = True
118
      if touching: continue
119
      break
120

121
  grid, output = common.grids(size, size)
122
  for idx in range(len(colors) // 4):
123
    for r in range(2):
124
      for c in range(2):
125
        grid[brows[idx] + r][bcols[idx] + c] = colors[idx * 4 + r * 2 + c]
126
        output[brows[idx] + r][bcols[idx] + c] = colors[idx * 4 + r * 2 + c]
127
    shadow = len(set(colors[idx * 4 : (idx + 1) * 4]))
128
    for r in range(shadow):
129
      for c in range(2):
130
        output[brows[idx] + r + 2][bcols[idx] + c] = common.green()
131
  return {"input": grid, "output": output}
132

133
This generator creates the input/output pairs that define the puzzle pattern.
134

135
Here is version 1 (208 bytes):
136
p=lambda g,R=range:(Z:=[(B,A,len({*f}))for B in R(9)for A in R(9)if all(f:=(g[B][A],g[B][A+1],g[B+1][A],g[B+1][A+1]))])and[g[C].__setitem__(slice(A,A+2),[3,3])for B,A,H in Z for I in R(H)if(C:=B+2+I)<10]and g
137

138
Here is version 2 (158 bytes):
139
def p(g):
140
 R=range
141
 for i in R(63):
142
  r=6-i//9;c=i%9
143
  f=g[r][c:c+2]+g[r+1][c:c+2]
144
  h=len({*f})*all(f)
145
  for j in R(h):g[r+2+j][c:c+2]=[3,3]
146
 return g
147

148
Here is version 3 (139 bytes):
149
def p(i):
150
 for t in range(63):
151
  a=6-t//9;t%=9;r=i[a][t:t+2]+i[a+1][t:t+2]
152
  for o in i[a+2:][:len({*r})*all(r)]:o[t:t+2]=3,3
153
 return i
154

155

156
The solutions show progressive improvement: from 208 bytes (version 1) to 139 bytes (version 3), saving 69 bytes total.
157
You should learn from this progressive improvement to further shorten the code that I care about in the current task. There is still room for improvement compared to the global best solution: 18 bytes can potentially be saved (from 139 to 121 bytes).
158

159

160
===
161
Task 261:
162

163
You are tasked with producing the **shortest possible Python solution (in bytes)** that passes all the given test cases.
164

165
The current global best solution size is 47 bytes.
36 collapsed lines
166

167
## Generator Function
168

169
This is the generator function used to create the puzzles that our solution function `p` is trying to solve for this specific task:
170

171

172
def generate(size=None, rows=None, cols=None):
173
  """Returns input and output grids according to the given parameters.
174

175
  Args:
176
    size: the width and height of the (square) grid
177
    rows: a list of vertical coordinates where pixels should be placed
178
    cols: a list of horizontal coordinates where pixels should be placed
179
  """
180
  if size is None:
181
    size = common.randint(3, 7)
182
    width = common.randint(size // 2, (size + 1) // 2)
183
    height = common.randint(size // 2, (size + 1) // 2)
184
    row = common.randint(0, size - height - 1)
185
    col = common.randint(0, size - width)
186
    while True:
187
      pixels = common.random_pixels(width, height, 0.5)
188
      if not pixels: continue
189
      rows, cols = zip(*pixels)
190
      rows, cols = [r + row for r in rows], [c + col for c in cols]
191
      break
192

193
  grid, output = common.grids(size, size)
194
  for r, c in zip(rows, cols):
195
    grid[r][c] = common.cyan()
196
    output[r + 1][c] = common.red()
197
  return {"input": grid, "output": output}
198

199

200
This generator creates the input/output pairs that define the puzzle pattern.
201

202
Here is version 1 (152 bytes):
203
def p(m):
204
 a=[[0 if v==8 else v for v in r]for r in m]
205
 [a[i+1].__setitem__(j,2)for i,r in enumerate(m[:-1])for j,v in enumerate(r)if v==8]
206
 return a
207

208

209
Here is version 2 (57 bytes):
210
p=lambda g:[*map(lambda r:[v>>2 for v in r],[g.pop()]+g)]
211

212

213
Here is version 3 (47 bytes):
214
p=lambda g:[[v%3for v in r]for r in[g.pop()]+g]
215

216

217
The solutions show progressive improvement: from 152 bytes (version 1) to 47 bytes (version 3), saving 105 bytes total.
218
You should learn from this progressive improvement to further shorten the code that I care about in the current task.
219

220

221
===
222

223

224
## Current Task
225
You are now given **Task 1** with test cases and a working solution.
226
Your objective: shorten the solution toward or beyond the global best size, while ensuring it still passes all test cases.
227

228
===
229
Task 1:
230

231
You are tasked with producing the **shortest possible Python solution (in bytes)** that passes all the given test cases.
232

233
The current global best solution size is 61 bytes.
66 collapsed lines
234

235
## Generator Function
236

237
This is the generator function used to create the puzzles that our solution function `p` is trying to solve for this specific task:
238

239

240
def generate(rows=None, cols=None, color=None, size=3):
241
  """Returns input and output grids according to the given parameters.
242

243
  Args:
244
    rows: a list of vertical coordinates where pixels should be placed
245
    cols: a list of horizontal coordinates where pixels should be placed
246
    color: a digit representing a color to be used
247
    size: the width and height of the (square) grid
248
  """
249
  if rows is None:
250
    pixels = common.sample(common.all_pixels(size, size), common.randint(2, 8))
251
    rows, cols = zip(*pixels)
252
    color = common.random_color()
253

254
  grid, output = common.grid(size, size), common.grid(size * size, size * size)
255
  for r, c in zip(rows, cols):
256
    grid[r][c] = color
257
    for rr, cc in zip(rows, cols):
258
      output[rr * size + r][cc * size + c] = color
259
  return {"input": grid, "output": output}
260

261

262
This generator creates the input/output pairs that define the puzzle pattern.
263

264

265
## Test Cases
266

267
**Example 1:**
268
Input:
269
[[0, 1, 1], [0, 0, 0], [0, 1, 1]]
270
Output:
271
[[0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1]]
272

273
**Example 2:**
274
Input:
275
[[0, 3, 3], [3, 3, 0], [0, 3, 3]]
276
Output:
277
[[0, 0, 0, 0, 3, 3, 0, 3, 3], [0, 0, 0, 3, 3, 0, 3, 3, 0], [0, 0, 0, 0, 3, 3, 0, 3, 3], [0, 3, 3, 0, 3, 3, 0, 0, 0], [3, 3, 0, 3, 3, 0, 0, 0, 0], [0, 3, 3, 0, 3, 3, 0, 0, 0], [0, 0, 0, 0, 3, 3, 0, 3, 3], [0, 0, 0, 3, 3, 0, 3, 3, 0], [0, 0, 0, 0, 3, 3, 0, 3, 3]]
278

279
**Example 3:**
280
Input:
281
[[0, 6, 0], [0, 0, 0], [0, 6, 6]]
282
Output:
283
[[0, 0, 0, 0, 6, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 6, 6, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 6, 0, 0, 6, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 6, 6, 0, 6, 6]]
284

285
**Example 4:**
286
Input:
287
[[0, 0, 1], [0, 0, 1], [1, 0, 0]]
288
Output:
289
[[0, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0, 0, 0, 0]]
290

291
**Example 5:**
292
Input:
293
[[0, 0, 5], [5, 0, 5], [0, 0, 0]]
294
Output:
295
[[0, 0, 0, 0, 0, 0, 0, 0, 5], [0, 0, 0, 0, 0, 0, 5, 0, 5], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 5, 0, 0, 0, 0, 0, 5], [5, 0, 5, 0, 0, 0, 5, 0, 5], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0]]
296

297
The test cases are generated by the `generate` function. You should make sure that the solution still passes all the test cases.
298

299

300
Here is the 1th working solution  (98 bytes):
301

302
p=lambda g:[[g[a][b]&g[c][d]for d in range(3)for b in range(3)]for c in range(3)for a in range(3)]
303

304

305
Here is the 2th working solution  (84 bytes):
306

307
p=lambda g:[[g[a//3][b//3]&g[a%3][b%3]for b in(0,1,2,3,4,5,6,7,8)]for a in range(9)]
308

309

310
This is the current best solution (61 bytes):
311

312
p=lambda g:[[A&C for A in A for C in B]for A in g for B in g]
313

314
This current best solution have 61 bytes, and the global best possible score is 58 bytes.
315
We want to improve the current solution to the global best possible score while keeping the same functionality.
316

317
You should not repeat the best solution code, and you should not repeat the working solution code. You should use all the insight and understanding of the working solution and the best solution to further shorten the code, and provide the shortened version of the code.

Context Engineering

This was where we spent most of our time: figuring out what information helps the agent reason effectively, and what causes the LLM to suffer from context rot or distraction.

We divided this into two key parts:

1. Prompt Construction for Solving ARC-AGI — information that helps the LLM produce a working solution to an ARC-AGI task.
2. Prompt Construction for Code Golfing — information that helps the LLM shorten or golf an already working solution.

Prompt Construction for Solving ARC-AGI

When I joined the competition, several existing community resources were already invaluable for bootstrapping first working solutions:

• arc-dsl — A Domain-Specific Language for ARC-AGI tasks, with a Python DSL file that defines composable primitives for common visual and logical transformations. While not comprehensive, these building blocks can express a large portion of ARC-AGI tasks. There’s also a solver module showing how to assemble complete solutions with the DSL.

• ARC-GEN — This repo contains the generator code for the ARC-AGI competition dataset. Each generator defines a family of puzzles with shared transformations. Although it doesn’t always expose the high-level pattern directly, it provides crucial signals to help the model infer the underlying rules and constraints.

To ground the model further, we included a few raw input→output pairs as plain matrices, e.g.:

1
**Example 1:**
2
Input:
3
[[0, 1, 1], [0, 0, 0], [0, 1, 1]]
4
Output:
5
[[0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1], [0, 0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 1, 1, 0, 1, 1]]

First-pass system prompt

With these components in place, here’s the first version of the system prompt I used:

1. System role (expert Python code-golfer for ARC-AGI)
2. Exemplar tasks
   • ARC-GEN generator snippet
   • arc-dsl solution
   • Working solutions from the evolutionary database
3. Focus task
   • ARC-GEN generator snippet
   • arc-dsl solution
   • Task examples (input→output pairs)
4. Output rules enforcing a short, single-function, working program for the focus task

This prompt solved about half the tasks without manual coding, even with a fast, non-flagship model (gemini-2.5-flash). However, progress plateaued. We traced this to a mismatch between arc-dsl assumptions and the ARC-GEN task distributions:

• Generator drift / artefacts: The competition included many extra examples per task generated from ARC-GEN, some deviating subtly from the “canonical” pattern that is described in the original arc-agi task.
• DSL shortcuts: Some arc-dsl solutions solved the original training/test grids via clever shortcuts, but didn’t generalize to the broader examples.

The upshot: arc-dsl sometimes confused the model on certain tasks. Our fix was simple but effective, we removed arc-dsl code from the prompt, keeping only ARC-GEN snippets.

After this pruning, the agentic loop resumed and reached ~360 solved tasks. For the remainder, I wrote manual solutions or adapted vetted public ones into the codebase.

Prompt Construction for Code Golfing

This is where we assembled a compact, high-leverage set of code-golf idioms.

Sourcing the idioms

I started by asking the model for generic Python golf tips. These were helpful, but shallow. Next, I searched community resources. Most code-golf sites only show solution lengths, not code, so transfer is limited. Eventually, I found an archived competition site: https://steffan153.github.io/wg-sol/. It has fewer than 50 problems; most aren’t matrix-heavy, but a few transfer well to ARC-AGI. The key: submissions are visible and ranked by length, so you can track the incremental byte-saving tricks. I used ChatGPT agent mode to crawl the archive and distill recurring patterns into prompt-ready snippets.

The Evolutionary DB as a teacher

Beyond the codebook, the Evolutionary DB turned out to be the best teacher for code golf. When a breakthrough happens—like a logic refactor that shaves bytes but preserves behavior—subsequent runs can retrieve that variant, and the model will often transfer the same motif to a different task with a similar pattern. In some cases, the transfer is almost direct. For example, Task 246 and Task 335 share the same pattern, differing only in numbers/colors:

ARC-AGI Example 246

Puzzle 246 of ARC-AGI: Extend the red dot rightward and the green dot upward with a blue trace; stop when they meet.

ARC-AGI Example 335

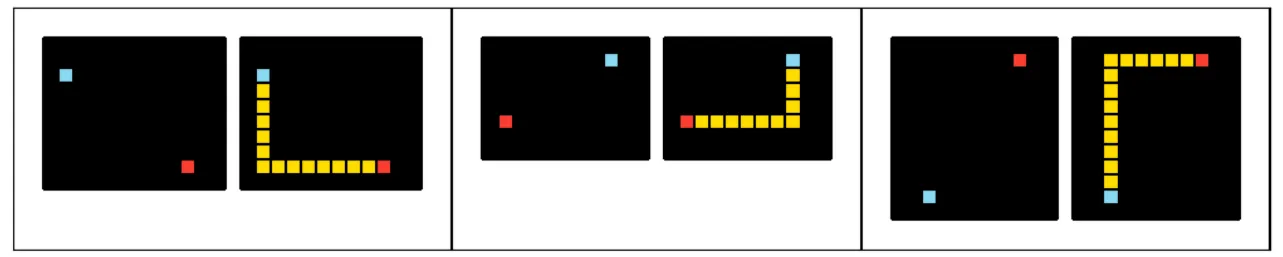
Puzzle 335 of ARC-AGI: Extend the red dot leftward and the blue dot downward with a yellow trace; stop when they meet.

So they are basically the same pattern.

Thanks to the Evolutionary DB-as-teacher approach, a breakthrough on one propagates to the other, so the final solutions are almost identical:

1
def p(g):
2
 D,E=sum(g,[]).index,divmod;F,C,A,B=E(D(3),(G:=len(g[0])))+E(D(2),G)
3
 while B-C:B+=B<C or-1;g[A][B]=8
4
 while A-F:g[A][C]=8;A+=A<F or-1
5
 return g

and

1
def p(g):
2
 D,E=sum(g,[]).index,divmod;F,C,A,B=E(D(8),G:=len(g[0]))+E(D(2),G)
3
 while B-C:B+=B<C or-1;g[A][B]=4
4
 while A-F:g[A][C]=4;A+=A<F or-1
5
 return g

This is an extreme example, but we frequently saw related patterns across tasks. That’s exactly where the Evolutionary DB shines in our agent.

Fighting context rot

We learned the hard way that too many input→output pairs, exemplars, and prior solutions can make the model drift. Early on, we used about 10 I/O pairs, 8 exemplars, and ~10 prior solutions per prompt—often blowing the context window. We pruned aggressively:

• I/O pairs: 10 → 5
• Cross-task exemplars: 8 → 3
• Prior solutions: 10 → 3 (and we shortened the long early arc-dsl solutions, which were often hundreds of lines)

Why fewer I/O pairs?

• Grids can be large (e.g., 28×28), and matrices are extremely token-inefficient: each digit, bracket, and comma is a token, so token count scales quickly.

Why fewer prior solutions?

• Early “working” solutions inherited from arc-dsl were often verbose scaffolding, with really long but working solution. Including too many consumed context and distracted the model.

Why fewer exemplars?

• More random exemplars increased the odds of hitting a useful match (tasks with similar patterns), but also injected noise.
• Instead, we added pattern tags per task (e.g., flood-fill, flip, extend rays, copy block), derived from the DSL’s modular sub-patterns. When sampling, we only retrieve pattern-similar tasks—cutting exemplars from 8 to 3 without losing relevance.

When scaling models stopped helping

About halfway through the competition (~1 month left, leaderboard ≈ 0.940xxx), we hit a ceiling. We tried switching to larger and newer models (qwen3-coder, kimi-k2, deepseek-R1, gemini-2.5-flash-lite → gemini-2.5-flash → gemini-2.5-pro) and expanded the “thinking budget” (12k → 32,768 tokens). But—no further shortenings.

At this point, neither prompt design nor retrieval was the bottleneck. The remaining tasks required fundamentally different logic—not just more “thinking.” I considered the agent to be saturated, merged into a team, and started manual coding to finish the tail.

Human-Injected Template Knowledge

While manual coding, we noticed recurring task families—for example, problems where the “natural” solution is DFS, BFS, flood-fill, or another grid search. From a code-golf perspective, these are painful: queues, boundary checks, four-direction neighbor sets, multi-line loops—the byte cost adds up fast. The good news is that many can be reframed in a much simpler way that compresses extremely well.

Here’s a detailed example showing how we (i) manually improved a working solution, (ii) abstracted that improvement into a template, and (iii) injected the template back into the agent so it could be reused elsewhere. This is a step outside the main agent loop, but the template is the key takeaway that powers future automated gains. We discovered several such templates throughout the competition, but here I’ll use Example 2 to demonstrate the process—this was my first manual breakthrough.

Example task (ARC-AGI Example 2):

The task: fill any zero (black) that is enclosed by 3s (green border) with 4 (yellow). Zeros that can “see” the border (via a path of zeros) should stay zero; all others turn to 4.

A natural solution: BFS/flood-fill. Here’s a baseline solution:

1
def p(g):
2
 R=range;l=len(g);q=[]
3
 for i in R(l):q+=[(i,0),(i,l-1),(0,i),(l-1,i)]
4
 while q:
5
  i,j=q.pop()
6
  if -1<i<l and -1<j<l and not g[i][j]:
7
   g[i][j]=1;q+=[(i+x,j+y)for x,y in((1,0),(-1,0),(0,1),(0,-1))]
8
 for i in R(l):
9
  for j in R(l):
10
   if not g[i][j]:g[i][j]=4
11
   elif g[i][j]==1:g[i][j]=0
12
 return g

What this 320-byte baseline does: It seeds a queue with border coordinates and flood-fills through zeros to mark everything reachable from the border. On the final scan:

• Zeros never reached by the flood-fill are enclosed → set to 4
• Zeros visited by the flood-fill are temporarily marked → restore to 0

This is robust but costly (in terms of byte): explicit queue, boundaries, four neighbors, multi-line loops.

The code-golf perspective: “rotate and erode”

Instead of growing a region from the border, we prefill and then erode exposure:

1. Prefill: Assume all zeros are enclosed and set them to 4.
2. Erode: Any 4 touching the outside via a chain of zeros is reverted to 0. We implement this by checking just the left neighbor and rotating the grid 90° each pass:
   • Pass 1: If the left neighbor is 0, the current 4 becomes 0 (exposed from the west).
   • Rotate 90°, repeat (north); again (east); again (south).
   • After four rotations, all directions are covered. Only truly enclosed cells remain 4.

This collapses BFS into a terse, single-expression update + rotate loop, which golfs extremely well.

Our 104-byte solution for Example 2 (“rotate and scan”):

1
p=lambda q,a=95:q*-a or p([*zip(*[map(lambda r,H:H*(H^4|r>0)or a//95*4,[0,*x],x)for x in q[::-1]])],a-1)

How the one-liner works:

• a is an iteration budget (multiple of 4 to fully sweep all directions, returning to original orientation).
• First pass: (a//95 == 1) prefill zeros to 4.
• Later passes: For each cell, if A==4 and left neighbor L==0, set A=0 (exposed).
• q[::-1] + zip(*) rotates the grid 90°, so a single left-neighbor rule is applied in all directions over four passes.

From one-off insight to reusable template

We saved 200 bytes by reframing the problem. But: simply dropping this solution into the Evolutionary DB wasn’t enough, as such “logic leaps” can confuse the LLM when reused cold. So we started to extract the pattern as a template, to be injected into the prompt when a similar task appears.

The reusable “rotate-and-update” template: Generalise the idea as a rotate-and-update loop: write a per-cell update that looks only “left”; rotation covers all directions. Still golf-friendly—no queues, single expression.

1
# n = iteration counter (keep n a multiple of 4 so orientation resets)
2
p=lambda o,n=95:-n*o or p(
3
 [*zip(*(
4
   ((A # <— replace with your per-cell update
5
    for L,A in zip((0,*r),r))
6
   for r in o[::-1]
7
  ))],-~n)

Examples for the update line:

• (A+(L==k)*(A<k)) # bump A if left is k
• (A,L)[cond] # choose L over A if condition met
• (x(A),A)[flag] # one-off transform

For Example 2, the per-cell update:

• First pass: zeros become 4
• Subsequent passes: if A==4 and L==0, set A=0 (erode)

This template typically saves 50–100 bytes per program for these task families. Stacking such templates produces large aggregate gains.

Why this matters for the agent: The point isn’t just manual golfing, it’s to harvest a template. Once crystallised, we inject the template into the agent’s system prompt. The Evolutionary DB then surfaces similar tasks, and the agent can reuse the motif automatically—turning a one-off breakthrough into a repeatable byte saver.

What didn’t work (and where we hand-golfed)

There was an ongoing discussion during the competition about what LLMs struggle with. Our experience mostly matched it:

• Regex never stuck. Even with templates and human-solved examples that used regex, the agent rarely synthesized a correct, byte-minimal regex. When regex was useful, we almost always had to hand-write it.
• Bitwise ops worked perfectly. When presented with multiple working solutions, the LLM reliably understood the logic and exploited bitwise operations wherever they applied.
• Recursion was fine—with a template. Once we built a solid template for recursion-related problems, the agent could use them reliably.
• Large logic pivots needed scaffolding. Whenever a breakthrough required a full reframing (like rotate-and-erode), the agent struggled, unless we packaged it as a reusable template and surfaced it via the Evolutionary DB.

Conclusion

That’s my slice of the system: a lean agentic loop, held together by Context Engineering and an Evolutionary DB, plus a handful of human-injected templates that traveled well. In parallel, my teammates explored other directions—compressing functions with zlib, AST-aware normalization to remove redundant characters, running smaller models augmented with better golf idioms, and even golfing with Claude Code. It was three months of steady grind, but deeply rewarding—and I learned a lot.

If you spot issues or want to build on this, I’ll publish the GitHub repo here once I finish tidying it up.

How to cite

BibTeX

1
@misc{mao2025golfingarcagi,
2
  title        = {Golfing ARC-AGI with a Lean Agentic Loop},
3
  author       = {Mao, Yuchen},
4
  year         = {2025},
5
  month        = {nov},
6
  howpublished = {\url{https://yuchen-mao.vercel.app/blog/google-code-golf}},
7
  note         = {Blog post}
8
}

Thanks for reading!